Práctica 3. Leyes de Kirchhoff

Objetivo:

Aplica las leyes de Kirchhoff en el análisis de circuitos eléctricos simples.

Materiales:

• ·        Formato de práctica

• ·        Computadora con Internet

• ·        Software de simulación

• ·        Cámara de video

• ·        2 resistencias de 2 Ohm

• ·        2 resistencias de 4 Ohm

• ·        1 resistencias de 3 Ohm

• ·        1 resistencias de 3k Ohm

• ·        1 resistencias de 2k Ohm

• ·        Una fuente de corriente de 10 V, una de 6V y dos de 4V.

• ·        Un conductor de 2mA
•           Voltímetro

Marco teórico:

Ley de los Voltajes de Kirchhoff. 

La sumatoria de los voltajes en una malla es igual a cero. Recordemos que cuando una corriente pasa por un elemento de circuito, en este caso una resistencia se produce una diferencia de potencial y se calcula mediante la ley de Ohm (V=IR).

Si multiplicamos las corrientes de malla por cada resistencia en la malla, al sumar los voltajes el total debe ser cero. Para asumir las corrientes de malla, necesitamos tener en cuenta que en un circuito eléctrico la corriente sale del positivo de la fuente y entra por el negativo de esta.

Si no hay una fuente de voltaje o de corriente en una malla entonces asumimos que la corriente fluye en un sentido horario.

Como primer paso se tiene que establecer la polaridad de cada elemento y la dirección de la corriente que fluye por cada malla del circuito.

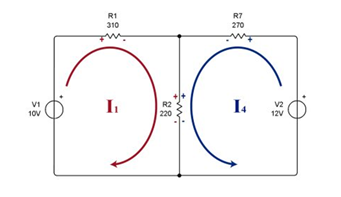
Cuando se polariza y se obtiene la trayectoria de las mallas se tiene que hacer una fórmula algebraica. Ejemplo:

∑ Voltajes de malla=0

-10V+310Ω+220Ω(I1)- 220Ω (I2) =0

Se simplifica la ecuación.

530Ω(I1)-220Ω(I2) =10V (Ecu 1)

∑ Voltajes de malla 4=0

-12V+270Ω(I4) +220(I4) +220(I1) =0

Se simplifica

490Ω(I4) +220Ω(I1) =12V (Ecu 2)

Ahora se resuelven por algún método algebraico y una vez obteniendo el resultado para I1 I4 se aplica la ley de Ohm para obtener el valor de Intensidad de corriente y el voltaje que existe en cada resistencia, así como la caída de voltaje.

Ley de Corriente de Kirchhoff:

Establece que la suma de todas las corrientes que salga de un nodo es igual a la corriente de este, es decir, algebraicamente la suma de las corrientes que pasan por el nodo será igual a cero. un nodo es un punto donde se cruzan dos o más elementos de circuitos, sea una fuente de voltaje o corriente, resistencias, capacitores, inductores, etc.

Para encontrar los voltajes el nodo 4 utilizamos el principio fundamental de la Ley de las Corrientes de Kirchhoff: la sumatoria de las corrientes que entran a un nodo es igual a la sumatoria de las corrientes que salen del nodo.

Para calcular el voltaje el nodo es necesario aplicar la siguiente fórmula, pero antes se tiene que dar una dirección a las corrientes del circuito. También es importante notar que todo circuito debe tener un nodo conectado a tierra y tendrá un valor de 0A.

∑corrientes de entrada = ∑ Corrientes de salida.

Para saber las corrientes que entran o salen de un nodo, utilizamos la Ley de Ohm. Según la Ley de Ohm, la corriente que pasa por una resistencia es igual a la diferencia de potencial entre la resistividad.

I=V/R

Con todo esto, se tiene que plantear una fórmula aplicando la ley de Ohm (I=V/R)

Desarrollo
Análisis de mallas.

1.- Se tiene que polarizar el circuito

2.-Se realizan las ecuaciones de cada malla:

3.-En este caso se resolverá el sistema de ecuaciones con el método de eliminación o igualación para conocer los valores de I1, I2 e I3:

4.-Se calculan las caídas de voltaje de todas las resistencias:

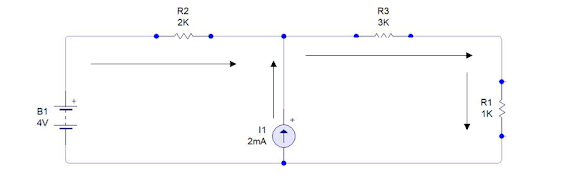
Análisis de nodos

1.- Se le da una dirección de corriente a cada rama.

2.-Se establece la ecuación para conocer el valor del nodo A:

3.-Se resuelven las ecuaciones y se obtiene el valor del nodo A:

4.-Se calcula la intensidad de corriente de cada segmento

5.-Con la ley de Ohm se obtiene las caídas de voltaje de las resistencias:

Video

Conclusiones

¿Cuáles fueron los retos o desafíos que enfrentaron? Y ¿Cuáles fueron sus aprendizajes adquiridos?

Los retos que enfrentamos nuevamente fue el desconocimiento del tema y la forma en que lo solucionamos fue repasando los videos y que cada uno realizará los circuitos para que pudiéramos comparar nuestros resultados de esta manera vimos quien estaba mal o bien.

Los aprendizajes fueron el entender de mejor manera el tema y saber en que momento y como se tiene que polarizar un circuito de mallas o nodos.